What are Diffusion Models?

As artificial intelligence continues to evolve, diffusion models have emerged as one of the most exciting and promising developments in the field of generative AI. These models have captured attention for their ability to create high-quality images, videos, and text from simple inputs. They are being utilized in a wide range of applications, from creative tasks to scientific breakthroughs.

However, while diffusion models are gaining popularity, many still struggle to understand how they work and how they can be effectively applied

In this blog, we will review a simple and intuitive explanation of the diffusion models, exploring how they function, and how you can use them.

What are diffusion models?

Diffusion models are a class of probabilistic generative model in machine learning, inspired by the concept of non-equilibrium thermodynamics in physics. They are considered one of the most promising AI developments of the last decade.

Some of the interesting applications of diffusion models include text-to-image and text-to-video generative AI models such as:

• OpenAI SORA
• Stable Diffusion by Stability AI
• Google Imagen

Diffusion models work by simulating a process where data is gradually corrupted with noise and then learning how to reverse this corruption to recover the original data. This reverse process is what allows diffusion models to generate new, high-quality samples. This is what makes them powerful tools for tasks like image generation, video synthesis, and more.

Diffusion models have emerged as the most popular invention since the Generative Adversarial Networks (GANs) in 2014.

Generative Adversarial Networks (GANs)

GANs are a class of probabilistic machine learning models that use an adversarial competition between a generator network that produces fake images resembling a target data distribution, and a discriminator network that distinguishes real images from the fake samples.

Consider the diffusion models to be a mathematical representation of a simulated diffusion process where energy spreads out due to temperature (gradients).

Let’s look at a few images produced by the diffusion model Google Imagen:

Generating something from nothing

Generative AI models, like large language models (LLMs), typically learn the underlying data distribution to generate new data. Some models, such as variational autoencoders, explicitly learn this distribution, while others, like GANs, generate samples implicitly without needing to learn the distribution upfront.

Additionally, generative models capture additional attributes, such as interdependencies between features in a data distribution, temporal dynamics for time series forecasting, and latent representations that highlight essential low-dimensional features, representing a high-dimensional data distribution, such as colors in an image instead of detailed objects.

Understanding the diffusion process

Diffusion models learn the noise-to-signal mapping of a data distribution, in the process of transitioning a true data distribution into pure noise and its reverse process (of reconstructing the original uncorrupted data distribution).

Consider the case of image generation with diffusion models:

Forward process

Noise is injected into an image sequentially for several timesteps until it becomes indistinguishable from pure noise. This is the forward process of the diffusion model, where an unknown data distribution is converted into a known prior distribution — pure noise, typically modeled by a Gaussian distribution with a defined mean and variance.

By understanding the parameters of this distribution (mean and variance), you can generate an infinite number of samples that belong to that distribution.

Reverse process

Starting from the pure noise distribution, the diffusion model learns to reconstruct the original data point by progressively removing the noise. This process occurs step-by-step, mirroring the way the model sequentially interacted with noise perturbations during the forward process.

There are several ways in which this reconstruction process is learned.

Common approaches to diffusion models

While there are various approaches to diffusion models, depending on the specific generative task and design, let’s discuss two common methods:

1. Denoising diffusion probabilistic models
2. Denoising score matching

Denoising diffusion probabilistic models

One common approach is for a neural network model to learn at each of the timestep, how much noise was introduced given the state of the noise-perturbed image at a given time step (going from pure noise to original image).

Denoising score matching

Another approach learns the gradient of the log-probability of noise-perturbed data points at every instance of the reverse process.

Intuitively, this information serves as a guide for removing the required noise perturbation at every time instance reaching from pure noise to the original data sample. It helps identify regions of the noisy space instead of the noise itself.

With this information, it guides the generative (reverse diffusion) process toward the direction of the true mean and variance of the original data sample.

Here is a visual representation of the forward process (first row) and the reverse process (second row):

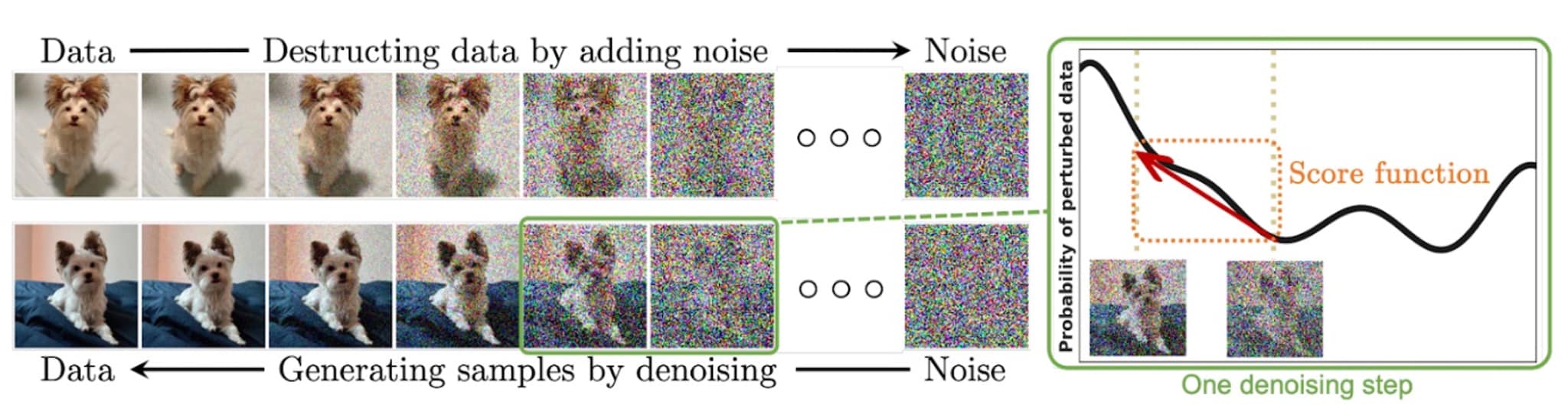
For a detailed mathematical explanation, follow the guides here and here.

Applications & use cases of diffusion models

Diffusion models are not just about generating creative images, videos and text in response to a user prompt. Diffusion models offer a variety of important applications in the domain of science, technology and business:

• Computational biology: AlphaFold 3 predicts molecular structures and interactions with a diffusion model. This is the latest iteration of the technology from the winners of the 2024 Nobel prize in chemistry.
• Time Series Imputation: Diffusion models can be used to generate missing information within time series data. This includes future forecasting (such as whether or stock pricing) and missing medical test results (such as transforming low resolution radiology results into high resolution and information-rich images)
• Chatbots: A variety of interactive multimodal chatbots on the market today use diffusion based generative processes.
• E-commerce: Prototyping new product designs, synthesizing images and videos for customer try-outs.
• Finance: Generate synthetic information to train fraud detection models.

What’s next for diffusion models?

There’s a lot more to do with regards to both the theoretical and empirical aspects of diffusion models research and applications. For example, the generative process is slower and therefore compute intensive. How can we develop more efficient sampling methods to generate new data?

These models are nevertheless powerful enough to emulate human behavior. This has already opened the doors for cybercriminals and can pose a security and privacy risk in the form of deepfakes and social engineering.